[자료구조 & 알고리즘] 공간 복잡도와 재귀함수란?

안녕하세요? 주니하랑 입니다.

오늘은 자료구조와 알고리즘의 공간 복잡도에 대해 공부 해 보도록 하는 것이에요.

소스 코드에 대해서 확인 하고 싶으신 분들께서는 주니하랑의 Git hub에 관심을 주세요!

 

 

---

 

 

 

📌 공간 복잡도 (Space Comploexity)

---

알고리즘에서 계산 복잡도를 계산할 때 두 가지를 고려하는 것이에요.

1. 시간 복잡도: 얼마나 빠르게 실행되는가?
2. 공간 복잡도: 얼마나 적은 저장 공간 용량을 사용하는가?

 

그렇기 때문에 좋은 알고리즘이란? 실행 시간도 짧고, 저장 공간도 적게 사용하는 것이겠지요?

 

하지만, 둘 다 만족 시키긴 어려운 것이에요.

왜냐하면? 시간과 공간은 완전하지는 않지만, 반 비례적 성향을 가지고 있기 때문이랍니다.

하지만 최근에는 대용량 System이 보편화되면서 공간 복잡도 보다는 시간 복잡도를 우선하는 경향이 있는 것이에요.

다만, Big Data와 같이 고용량을 다루는 업계에서는 당연히 공간 복잡도도 고려 한다는 것 잊지 마세요!

결국 알고리즘은 시간 복잡도가 중요하다고 정리할 수 있겠네요!

 

    📍 공간 복잡도는 대략적인 계산이 필요하답니다.

예전에 만들어졌던 공간 복잡도에 관한 고려 사항 문제들이 기존 알고리즘 문제에 많이 녹아 있는 것이에요.

그렇기 때문에 기존 알고리즘 문제에 시간 복잡도 뿐만 아니라, 공간 복잡도 제약 사항이 문제로 나오는 경우가 많다고 합니다.

또한, 기존 알고리즘 문제에 영향을 받으신 예전에 취업한 선배 개발자 분들이 면접에서 공간 복잡도에 대해 묻는 경우도 꽤 있다고 해요!

 

 

    📍 자세히 알아보기

Program을 실행 및 완료하는데, 필요한 저장공간의 양을 바로 공간 복잡도로 계산하는 것이에요.

총 필요 저장 공간은 어떻게 계산할까요?

1. 고정 공간 (알고리즘과 무관한 공간) : Code 저장 공간, 단순 변수 및 상수가 사용
2. 가변 공간 (알고리즘 실행과 관련한 공간) : 실행 중 동적으로 필요한 공간
3. $ S(P) = c + S_p(n) $
   • 여기서 c = 고정 공간
   • 여기서 $ S_p(n) $ = 가변 공간을 나타냄

 

 

 

    📍 공간 복잡도 계산법은 무엇일까요?

공간 복잡도 계산은 알고리즘에서 실제 사용되는 저장 공간을 계산하면 되는 것이에요.

이를 Big O 표기법으로 표현할 수 있다면 된답니다!

 

 

          👉 공간 복잡도 예제 1

n! (Factorial) 구하기

공식 : n! = 1 x 2 x 3 x ... x n

n의 값에 상관없이 변수 n, 변수 fac, 변수 index와 같이 세 개의 변수만 필요한 것이에요.

결국 변수가 각각 하나씩 필요한 것이닌까 공간 복잡도는 O(1)이 되는데, 이는 실제 알고리즘 실행 시 사용되는 저장 공간을 계산하면 되는 것이에요.

 

def factorial(data):
    fac_num = 1
    round_num = 0

    start_factorial_time = time.time()

    for index in range(2, data + 1):
        fac_num = fac_num * index
        round_num += 1
        print(str(round_num) + "번째 factorial 값은 \"" + str(fac_num) + "\" 입니다.")

    print("Factorial 계산 간 걸린 시간은 " + str(time.time() - start_factorial_time) + "초 입니다.")
    print("\n")
    return fac_num
    
    
    
print(factorial(3))

# 결과 6

 

 

          👉 공간 복잡도 예제 2

 

n! (Factorial) 구하기

공식 : n! = 1 x 2 x 3 x ... x n

이번에는 재귀함수를 사용해 볼 것이에요. n에 따라, 변수 n이 n개가 만들어지는 것이에요.

Factorial Function을 재귀 함수로 1까지 호출하였을 때, n 부터 1까지 Stack에 쌓이게 된답니다.

결국 공간 복잡도는 O(n)이 되겠네요!

 

def factorial_recursion(data):

    if data > 1:
        a = data * factorial_recursion(data - 1)

        return a

    else:
        return 1

 

Complexity:

expected worst-case time complexity : O(N)
expected worst-case space complexity: O(N)

 

 

 

 

📌 재귀 용법(Recursive call, 재귀 호출)

---

고급 정렬 알고리즘에서는 재귀 용법을 많이 사용하는 것이에요.

그래서 고릅 정렬 알고리즘을 공부하기 전에 주니하랑은 재귀 용법을 공부하기로 합니다!

 

재귀 용법은 함수 안에서 동일한 함수(자기 자신)을 호출하는 형태인 것이에요.

여러 알고리즘 작성 시에 사용되기 때문에 익숙해져야 한다고 합니다!

 

 

    📍 예제

• Factorial을 구하는 알고리즘을 Recursive Call을 이용하여 풀어보자!

 

 

 

          👉 예제 분석

1. 간단한 것부터 생각하기
   • 2! = 1 X 2
   • 3! = 1 X 2 X 3
   • 4! = 1 X 2 X 3 X 4
2. 반복되는 규칙 생각 해 보기 :
   
   • n! = n X (n -1)!
     예를 들어 4라면 4 = 4 X 3! 즉, 자기 자신에서 1 뺀 값들을 곱하는 규칙이 보인다.
   • 함수 만들기
   • 함수(n)은 n > 1 이면 return n X 함수(n -1)
   • 함수(n)은 n = 1 이면 return n
3. 검증 (코드로 부터 검증하지 않고, 직접 간단한 경우부터 대입해서 검증해야 하는 것!)
   • 2! 검증하기!
     • 함수(2) 이면, 2 > 1이기 때문에 2 X 함수(1)
     • 함수(1)은 1과 같기 때문에 조건문에 맞지 않는다 결국 return n이 되면서 반환이 이뤄질 것이고, 이럴 경우 return 2 X 1 = 2가 된다.
   • 3! 검증하기!
     • 함수(3) 이면, 3 > 1이기 때문에 3 X 함수(2)
     • 함수(2)는 결국 1번에 의해 2! 이므로, return 2 X 1 =2
     • 3 X 함수(2) = 3 X 2 = 3 X 2 X 1 = 6이 된다.
   • 4! 검증하기!
     • 함수(4)이면, 4 > 1이기 때문에 4 X 함수(3)
     • 함수(3)은 2번에 의해 3 X 2 X 1 = 6이 된다.
     • 4 X 함수(3) = 4 X 6 = 24가 된다.

 

 

          👉 Python

def factorial(n):
    if n > 1:
        return n * factorial(n - 1)

    else:
        return n
        
for num in range(10):
    print(factorial(num))
    
# 결과 : 0
#		1
#		2
#		6
#		24
#		120
#		720
#		5040
#		40320
#		362880

 

 

          👉 시간 복잡도와 공간 복잡도

factorial(n)은 n - 1번의 factorial()을 호출하여 곱셉을 하는 것이에요.

일종의 n - 1번 반복문을 돌리는 것과 같다고 볼 수 있겠네요!!

factorial() 함수를 호출할 때마다, 지역변수 n이 생기는 것이에요.

결국 시간 복잡도 / 공간 복잡도는 O(n - 1)이 되는데, Big O 표기법에서는 뒤에 부분을 잘라버리게 때문에 O(n)이 되는 것이랍니다!

 

 

 

    📍 재귀 호출의 일반적인 형태

# 일반적인 형태1
def function(입력):
    if 입력 > 일정값: # 입력이 일정 값 이상이면
        return function(입력 - 1) # 입력보다 작은 값
    else:
        return 일정값, 입력값, 또는 특정값 # 재귀 호출 종료

 

# 일반적인 형태2
def function(입력):
    if 입력 <= 일정값:              		 # 입력이 일정 값보다 작으면
        return 일정값, 입력값, 또는 특정값   # 재귀 호출 종료
    function(입력보다 작은 값)
    return 결과값

 

def factorial_reverse(n):
    if n <= 1:
        return n

    else:
        return n * factorial_reverse(n - 1)
        
        
for num in range(10):
    print(factorial_reverse(num))
    
    
    
# 결과 : 0
#		1
#		2
#		6
#		24
#		120
#		720
#		5040
#		40320
#		362880

 

 

 

          👉 재귀 호출관련 Stack

함수는 내부적으로 Stack처럼 관리 됩니다!

 

 

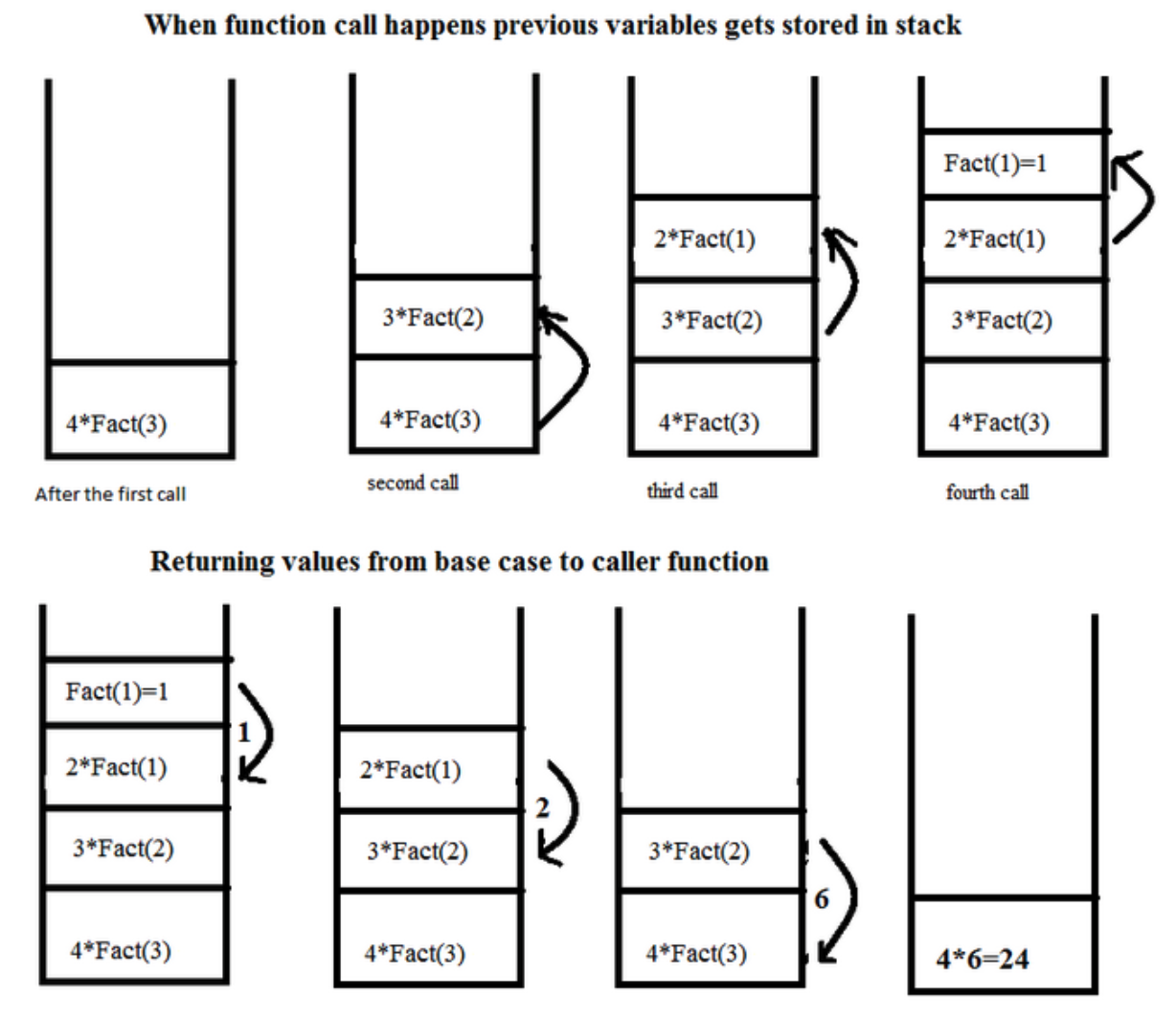
재귀 호출에 대해 잘 이해가 되지 않는다면 이 곳을 참고 해 보는걸 추천 드리는 것이에요!

참고로 파이썬은 내부적으로 Stack을 1000회 까지 Limit을 걸어 놓은 것이에요. 그렇기 때문에 배귀 함수 깊이(한번에 호출되는 횟수)가 1000회 이하여야 하고, 이 이상을 넘으면 Error가 난다고 합니다!

 

 

---

 

 

주니하랑의 글이 마음에 드셨나요? 구독과 공감! 그리고, 댓글은 주니하랑에게 많은 힘이 됩니다