2021. 9. 9. 08:00ㆍ코딩 테스트 준비/알고리즘
안녕하세요? 주니하랑 입니다.
오늘은 자료구조와 알고리즘의 알고리즘에서 동적 계획법과 분할 정복에 대해 공부 해 보도록 하는 것이에요.
소스 코드에 대해서 확인 하고 싶으신 분들께서는 주니하랑의 Git hub에 관심을 주세요!
📌 개요
📍동적 계획법이란?
Dynamic Programming을 줄여서 DP라고 많이 부른다고 해요!
동적 계획법은 입력 크기가 작은 부분 문제들을 해결한 뒤, 해당 부분 문제의 해(답)을 활용하여 보다 큰 크기의 부분 문제를 해결함으로, 최정적으로 전체 문제를 해결하는 알고리즘인 것이에요.
동적 계획법은 상향식 접근법으로, 가장 최하위 해답을 구한 뒤, 이를 저장하고, 해당 결과값을 이용하여 상위 문제를 풀어가는 것이에요.
또한, 문제를 잘게 쪼갤 때, 부분 문제는 중복이 되기 때문에 재활용이 가능하답니다!
- 문제의 예 : 피보나치 수열
👉 Memoizaion 기법 활용
- Memoization(메모이제이션) : 프로그램 실행 시 이전에 계산한 값을 저장. 이를 다시 계산하지 않도록 다음 계산에서 이 저장한 값을 활용하여 연산을 하도록 하는 것으로, 전체 실행 속도를 빠르게 하려고 사용하는 기술
📍분할 정복이란?
분할 정복은 문제를 나눌 수 없을 때까지 나누어서 각각을 풀면서 다시 그 결과를 다시 합병하여 문제의 답을 얻는 알고리즘인 것이에요.
하양식 접근법으로, 상위의 해답을 구하기 위해, 아래로 내려가면서 하위의 해답을 구하는 방식이랍니다.
이것은 일반적으로 재귀함수를 통해 구현하는 것이에요.
또한, 문제를 잘게 쪼갤 때, 부분 문제는 서로 중복되지 않는다는 특징이 있는 것이에요.
📍공통점과 차이점
👉 공통점
문제를 잘게 쪼개어 가장 작은 단위로 분할 시키는 점
👉 차이점
- 동적 계획법
- 부분 문제는 중복되어, 상위 문제 해결 시 재활용
- Memoization 기법 활용 (부분 문제의 해답을 저장하여 재활용하는 최적화 기법 사용)
- 분할 정복
- 부분 문제는 서로 중복되지 않음
- Memoization 기법 활용 하지 않음
📌 동적 계획법 알고리즘 이해
📍피보나치 수열이란?
피보나치 수열을 쉽게 설명하자면 앞에 항과 뒤에 항을 더하여 다음 항에 적고, 그것을 다시 앞에 항과 자신의 항을 더하여 뒤에 적음을 반복하는 것이에요. 이를 공식으로 표현하자면 $F0=0, F1=1, Fn+2=Fn+1+Fn$ 이렇게 점화식으로 정의할 수 있는 것이에요.
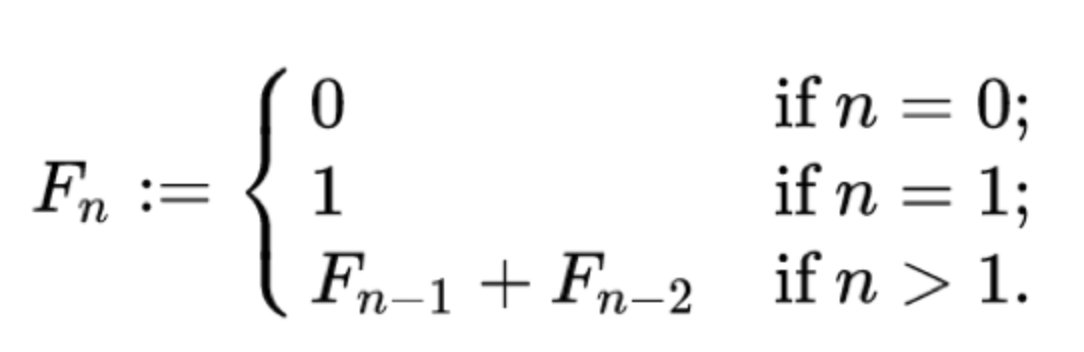
먼저 0번째와 1번째는 무조건 0과 1이 나오는 것이에요.
그런 뒤 2번째 부터는 앞에 항과 앞에 전의항을 더한 뒤 그것을 앞에 항 뒤에 적어주면 되는 것이에요.
이것을 함수로 표현해보고자 할 때, fibonacci라고 한다면
fibonacci(0):0
fibonacci(1):1
fibonacci(2):1
fibonacci(3):2
fibonacci(4):3
fibonacci(5):5
fibonacci(6):8
fibonacci(7):13
fibonacci(8):21
fibonacci(9):34

위의 그림처럼 만약 함수에 6이라는 값을 넣었다면 어떻게 될까요?
6은 함수(4)와 함수(5)로 쪼갤 수 있게 될 것이고, 또 함수(4)는 함수 (2)와 함수 (3)으로, 쭉쭉 쪼개지게 될 것이에요.
### recursive Call 활용
def fibonacciRec(num):
if num <= 1:
return num
return fibonacciRec(num - 1) + fibonacciRec(num - 2)
print(fibonacciRec(4))
# 결과값 : 3
먼저 4를 입력하게 되면 num(4)는 1보다 크기 때문에 return문으로 바로 갈 것이에요.
return문은 재귀함수를 통해 fibonacciRec 함수에 num - 1 즉, 4 - 1을 해서 호출이 되고, 또, num - 2 즉, 4 - 2를 호출하고 있답니다.
위에서 이야기 했듯 함수(4)를 두 개로 쪼갠 것이고, 함수(2)와 함수(3)이 호출되면서 쪼개지는 것을 볼 수 있는 것이에요.
그렇게 3과 2가 각각 또 num으로 들어가서 쪼개지기를 반복하는 것이랍니다.
그런 뒤 반환될 때 이 값들이 더해지면서 값이 나오게 되는 것이에요.
### 동적 계획법(Dynamic Programming) 활용
def fibonacci_dp(num):
cache = [0 for index in range(num + 1)]
cache[0] = 0
cache[1] = 1
for index in range(2, num + 1):
cache[index] = cache[index - 1] + cache[index - 2]
print(cache)
return cache[num]
print(fibonacci_dp(10))
# 결과값 : 55
좀 더 보기 쉽게 코드를 분석하고자 한다면 여기를 클릭하셔서 해 보실 수 있답니다!
'코딩 테스트 준비 > 알고리즘' 카테고리의 다른 글
| [알고리즘] Quick Sort (퀵 정렬) (0) | 2021.09.09 |
|---|---|
| [알고리즘] 병합 정렬 (merge sort) (0) | 2021.09.09 |
| [알고리즘] 02. 선택 정렬 (0) | 2021.09.08 |
| [알고리즘] 01. 버블정렬 (0) | 2021.09.07 |
| [알고리즘] 00. 알고리즘 연습 방법 (0) | 2021.09.06 |